Use proper math syntax during question authoring
Proper mathematical syntax is required while defining the correct answer of a question during Möbius question authoring.
NOTE: Similarly, students are required to enter their responses with proper mathematical syntax.
The following types of mathematical entries require particular syntax styling in order for Möbius to correctly interpret your defined correct answer:
- Mathematical expressions
- Variable names
- Function and operator syntax
Some notation applies to all of Möbius, while others apply specifically to Maple Syntax.
Maple Syntax — The language that the MapleTM math engine uses to interpret mathematical expressions.
NOTE: Maple-graded questions use Maple Syntax logic for grading student responses.
Mathematical expression syntax
When entering formulas and expressions as the correct answer to a question, use standard mathematical notation that's similar to that used by a graphing calculator (Example — (x^2-2*x+1)*2*sin(x)*(x^2+1)*e^(-x^2) is accepted).
Here are some notes on using mathematical expression syntax when defining your correct answer:
- Place the argument of a function in parentheses () (Example — enter sqrt(3x) not sqrt 3x, which is interpreted as (sqrt(3))*x).
- Be sure to include parentheses () (Example — the expression 1/(x+1) is different from 1/x+1 which Möbius interprets as
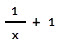 ).
).
Variable name syntax
The variable(s) in your defined correct answer must be identical—this includes case sensitivity—to the variable(s) used in the question statement.
If these don't match, your students will be confused on how to enter the correct response. Example — If the question uses the variable t, but you've defined the correct answer using T, students who use t in their response will be graded as incorrect.
TIP: Check out the Syntax rules for variables section in the Algorithm Editor syntax rules help topic for more tips on using algorithmic variables in your question.
Function and operator syntax
Jump to section
Functions and operators require specific syntax when they're used while defining the correct answer.
The required syntax varies depending on whether you're authoring with Möbius syntax or using Maple syntax.
IMPORTANT: Maple syntax is needed when:
- Authoring Maple-graded questions
- Using the maple command in the Algorithm pane
When authoring a Maple-graded Maple syntax question sub-type, be sure to inform your students that Maple syntax is required.
TIP: Remember to preview your authored question to ensure that you've defined the correct answer using the accepted math syntax.
Arithmetic
| Arithmetic | Syntax for Möbius or Maple |
|---|---|
| Addition | + |
| Subtraction | - |
| Multiplication | * |
| Division | / |
| Exponentiation | ^ |
TIP: Alternatively, for multiplication with Möbius syntax, you can use:
- Two letters with a space (Example — x y)
- A letter and a number with or without a space (Example — 2x or 2 x)
However, for multiplication with Maple syntax, you must include an asterisk (*) (Example — 2*x and not 2x; x*y and not xy; x*y and not x y).
Trigonometric functions
| Function | Syntax for Möbius or Maple |
|---|---|
| Sine | sin |
| Cosine | cos |
| Tangent | tan |
| Inverse sine | arcsin |
| Inverse cosine | arccos |
| Inverse tangent | arctan |
| Secant | sec |
| Cosecant | csc |
| Cotangent | cot |
NOTE: Arguments of trigonometric functions are evaluated in radians. The results of the inverse trigonometric functions are evaluated in radians.
Hyperbolic trigonometric functions
| Function | Möbius syntax | Maple syntax |
|---|---|---|
| Hyperbolic sine | hypsin | sinh |
| Hyperbolic cosine | hypcos | cosh |
| Hyperbolic tangent | hyptan | tanh |
| Hyperbolic secant | hypsec | sech |
| Hyperbolic cosecant | hypcsc | csch |
| Hyperbolic cotangent | hypcot | coth |
| Inverse hyperbolic sine | archypsin | arcsinh |
| Inverse hyperbolic secant | archypsec | arcsech |
| Inverse hyperbolic cosecant | archypcsc | archcsch |
| Inverse hyperbolic cotangent | archypcot | arccoth |
NOTE: Arguments of trigonometric functions are evaluated in radians. The results of the inverse trigonometric functions are evaluated in radians.
Numbers and constants
| Number or constant | Möbius syntax | Maple syntax |
|---|---|---|
| 2.71828... | e | exp(1) |
| 3.14159... | Pi | Pi |
| Scientific notation | E | E |
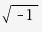 | N/A* | I |
NOTE: The variable e shouldn't be assigned as a global variable in Maple code. However, it can be used as a local variable.
TIP: The E for scientific notation is entered between the coefficient and the order of magnitude. Example — 290,000,000 would be 2.9E8.
NOTE: For the square root of -1, it's a capital letter i.
Functions
| Function | Möbius syntax | Maple syntax |
|---|---|---|
| Limit of a function ƒ | N/A* | limit(f, x=a) |
| Derivative or partial derivative of a function ƒ | N/A* | diff(f, x) |
| Integral of a function ƒ | N/A* | int(f, x) |
| Absolute value | abs(x) | abs(x) |
| Square root | sqrt(x) or x^(1/2) | sqrt(x) or x^(1/2) |
| Exponential | e^x | exp(x) |
| Logarithm base b | N/A* | log[b](x) |
| Logarithm base 10 | log(x) | log10(x) |
| Natural logarithm (base e) | ln(x) | log(x) or ln(x) |
IMPORTANT: Students aren't able to tell if the response to your Maple-graded question requires Maple syntax or not when using the text entry mode. It's recommended that you specify in the question statement of your Maple-graded question that:
- log[10] in Maple is interpreted as log base 10
- log in Maple is interpreted as log base e