Calculus III for Honours Mathematics

Created by: University of Waterloo, powered by Möbius

Description

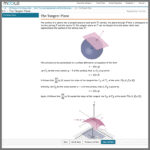
The Calculus III for Honours Mathematics Content Pack is a Möbius course developed by the University of Waterloo that you can use as a customizable starting point to a complete multivariable calculus course in Möbius. This Content Pack is presented with a theoretical and proofs-based approach. Topics covered include: calculus of functions of several variables, limits, continuity, differentiability, the chain rule, the gradient vector and the directional derivative, Taylor’s formula, optimization problems, mappings and the Jacobian, and multiple integrals in various coordinate systems. This customizable resource contains 17 units containing sectioned lessons and assignments enhanced with Möbius capabilities including in-lesson questions with unlimited practice, algorithmic questions, adaptive questions, Geogebra resources, interactive narratives, hints and immediate feedback, and end-of-section assignments.

How does Möbius take the University of Waterloo’s content to the next level?

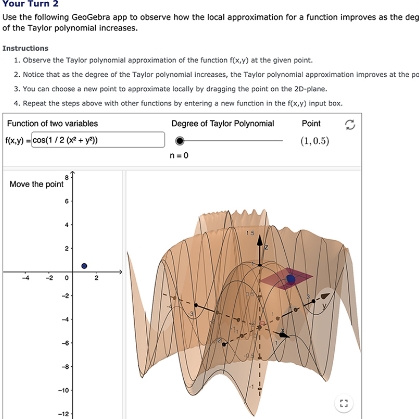
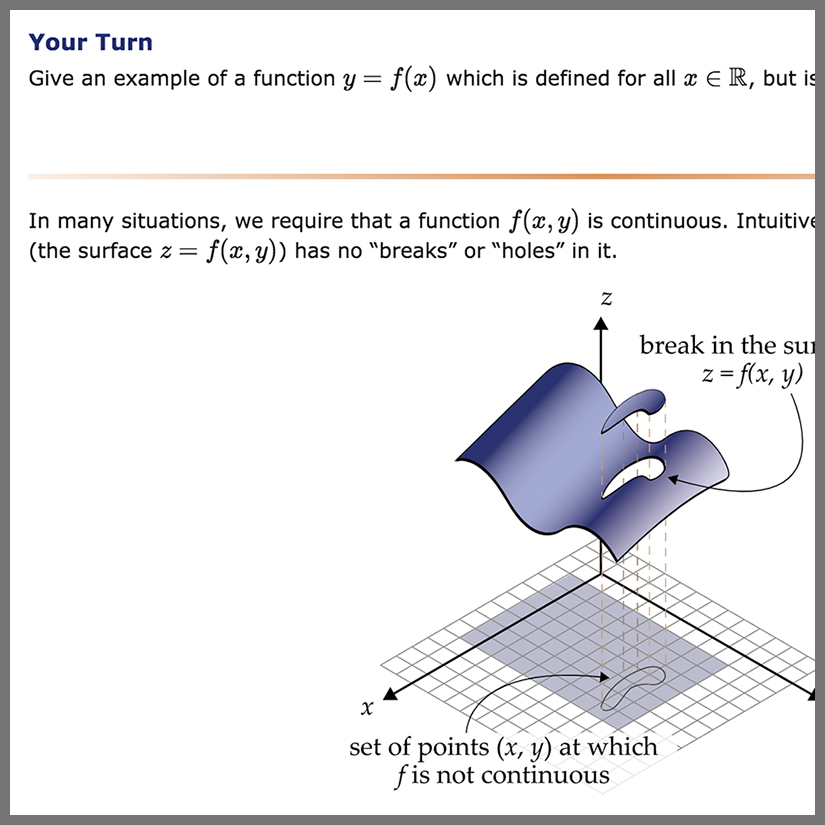
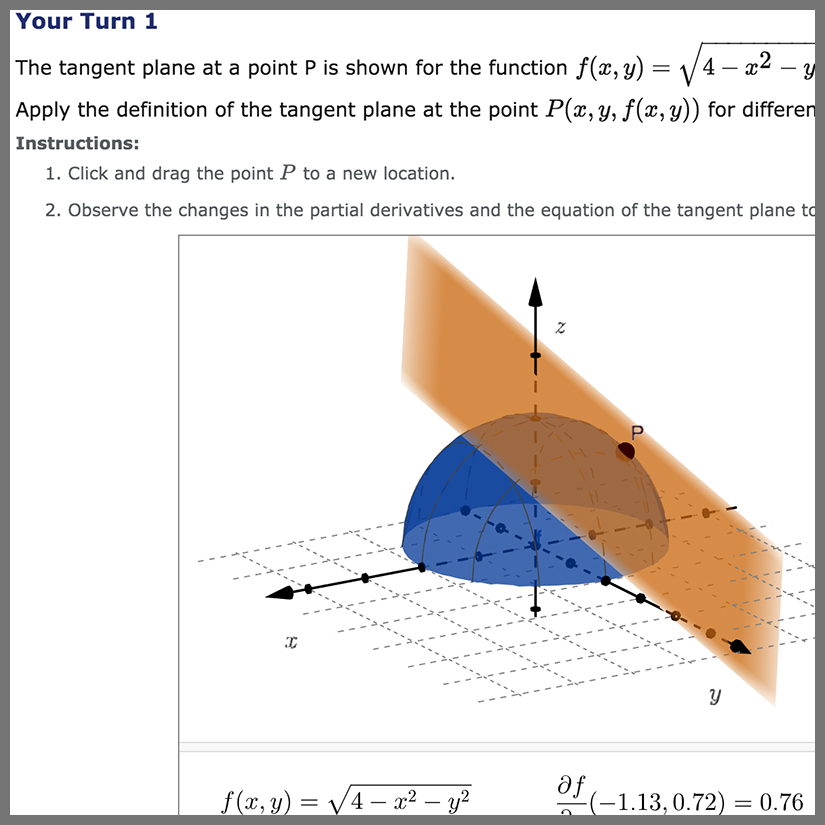
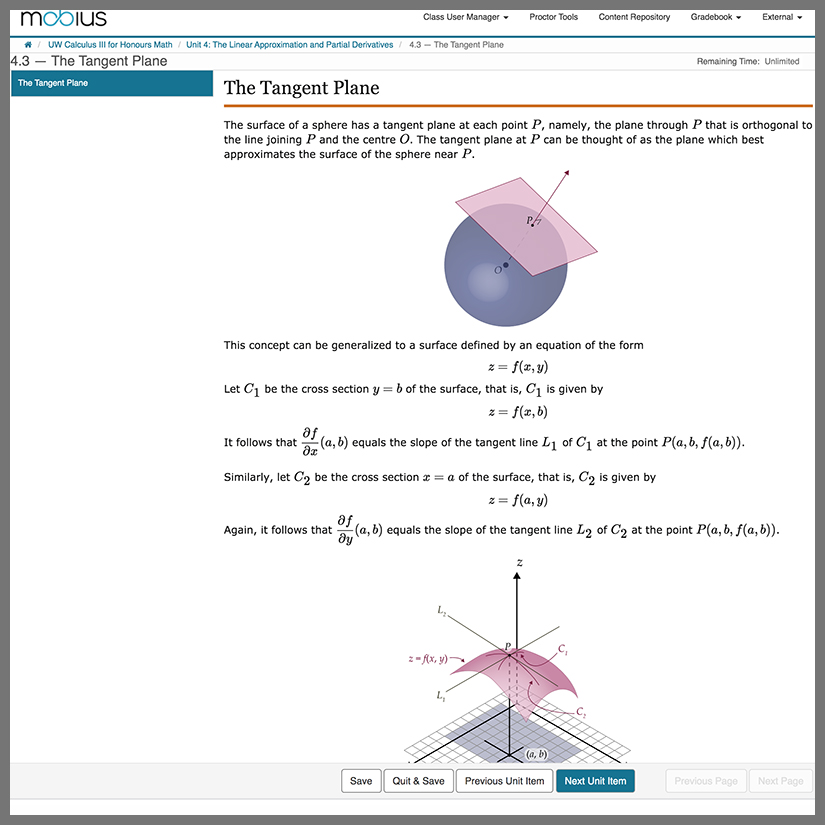
  • Lessons contain interactive elements like Interactive Narratives, HTML objects, Math Apps, or Geogebra applications to help solidify difficult STEM concepts.

  • Learn how Möbius’ unique STEM question types throughout this content provide the best STEM learning experience.

  • Work with over 50 configurable assessment properties when modifying existing or building your own assessments.

Course Structure

  • All content is organized into 17 units for easy navigation
  • Course materials provide a solid foundation for creating your course offering which include 65 lessons that promote Active Learning by including illustrative visualizations, interactive elements, and example problems with immediate feedback
  • Different forms of assessment materials are distributed across 12 assignments to evaluate student comprehension through a variety of different question types
  • Pull from a vast selection of over 400 questions that you can use to create your own lessons and assignments or supplement existing ones
17 units
65 lessons
12 assignments
400+ questions

Unit 0: Getting Started

Unit 1: Graphs of Scalar Functions

  • 1.1 Scalar Functions

  • 1.2 Geometric Interpretation of z = f(x, y)

  • 1.3 Putting It All Together

Unit 2: Limits

  • 2.1 Definition of a Limit

  • 2.2 Limit Theorems

  • 2.3 Proving a Limit Does Not Exist

  • 2.4 Proving a Limit Exists

  • 2.5 Appendix: Inequalities and Absolute Values

  • 2.6 Putting It All Together

Unit 3: Continuous Functions

  • 3.1 Definition of a Continuous Function

  • 3.2 The Continuity Theorems

  • 3.3 Putting It All Together

Unit 4: The Linear Approximation

  • 4.1 Partial Derivatives

  • 4.2 Higher-Order Partial Derivatives

  • 4.3 The Tangent Plane

  • 4.4 Linear Approximation for z = f(x, y)

  • 4.5 Linear Approximation in Higher Dimensions

  • 4.6 Putting It All Together

Unit 5: Differentiable Functions

  • 5.1 Definition of Differentiability

  • 5.2 Differentiability and Continuity

  • 5.3 Continuous Partial Derivatives and Differentiability

  • 5.4 The Linear Approximation Revisited

  • 5.5 Putting It All Together

Unit 6: The Chain Rule

  • 6.1 Basic Chain Rule in Two Dimensions

  • 6.2 Extensions of the Basic Chain Rule

  • 6.3 The Chain Rule for Second Partial Derivatives

  • 6.4 Putting It All Together

Unit 7: Directional Derivatives and the Gradient Vector

  • 7.1 Directional Derivatives

  • 7.2 The Gradient Vector in Two Dimensions

  • 7.3 The Gradient Vector in Three Dimensions

  • 7.4 Putting It All Together

Unit 8: Taylor Polynomials and Taylor’s Theorem

  • 8.1 The Taylor Polynomial of Degree 2

  • 8.2 Taylor’s Formula with Second Degree Remainder

  • 8.3 Generalizations of the Taylor Polynomial

  • 8.4 Putting It All Together

Unit 9: Critical Points

  • 9.1 Local Extrema and Critical Points

  • 9.2 The Second Derivative Test

  • 9.3 Convex Functions

  • 9.3 Proof of the Second Partial Derivative Test

  • 9.4 Putting It All Together

Unit 10: Optimization Problems

  • 10.1 Extreme Value Theorem

  • 10.2 Algorithm for Extreme Values

  • 10.3 Optimization with Constraints

  • 10.4 Putting It All Together

Unit 11: Coordinate Systems

  • 11.1 Polar Coordinates

  • 11.2 Cylindrical Coordinates

  • 11.3 Spherical Coordinates

  • 11.4 Putting It All Together

Unit 12: Mappings of R2 into R2

  • 12.1 The Geometry of Mappings

  • 12.2 The Linear Approximation of a Mapping

  • 12.3 Composite Mappings and the Chain Rule

  • 12.4 Putting It All Together

Unit 13: Jacobians and Inverse Mappings

  • 13.1 The Inverse Mapping Theorem

  • 13.2 Geometrical Interpretation of the Jacobian

  • 13.3 Constructing Mappings

  • 13.4 Putting It All Together

Unit 14: Double Integrals

  • 14.1 Definition of Double Integrals

  • 14.2 Iterated Integrals

  • 14.3 The Change of Variable Theorem

  • 14.4 Putting It All Together

Unit 15: Triple Integrals

  • 15.1 Definition of Triple Integrals

  • 15.2 Iterated Integrals

  • 15.3 The Change of Variable Theorem

  • 15.4 Putting It All Together

Möbius Assignments

Back to Menu

Want a closer look at this Content Pack?

Our Möbius experts can show you the capabilities of any of our Content Packs. During this complimentary, customized demonstration, you’ll discover how Möbius can elevate your online course delivery for STEM subjects.

Contact us to Learn More

Content Packs That May Interest You

Introduction to Differential Equations

Linear Algebra I

Calculus Volume 3

Browse Content Catalogue

Experience Möbius from
your students’ perspective

Try it Now
DigitalEd