Calculus Volume 1

Created by: OpenStax, powered by Möbius

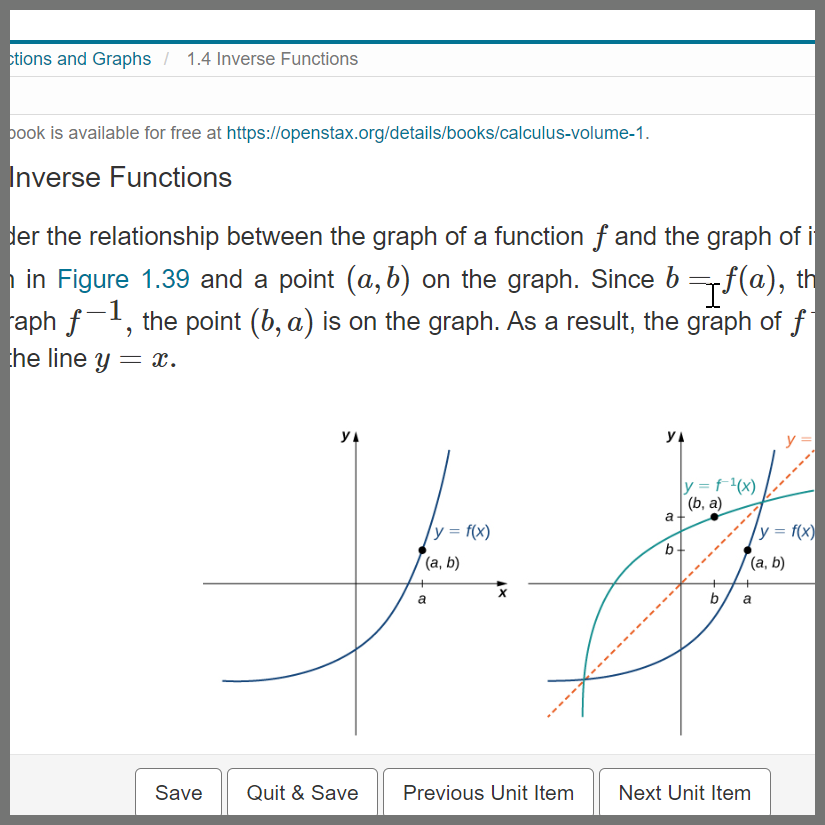
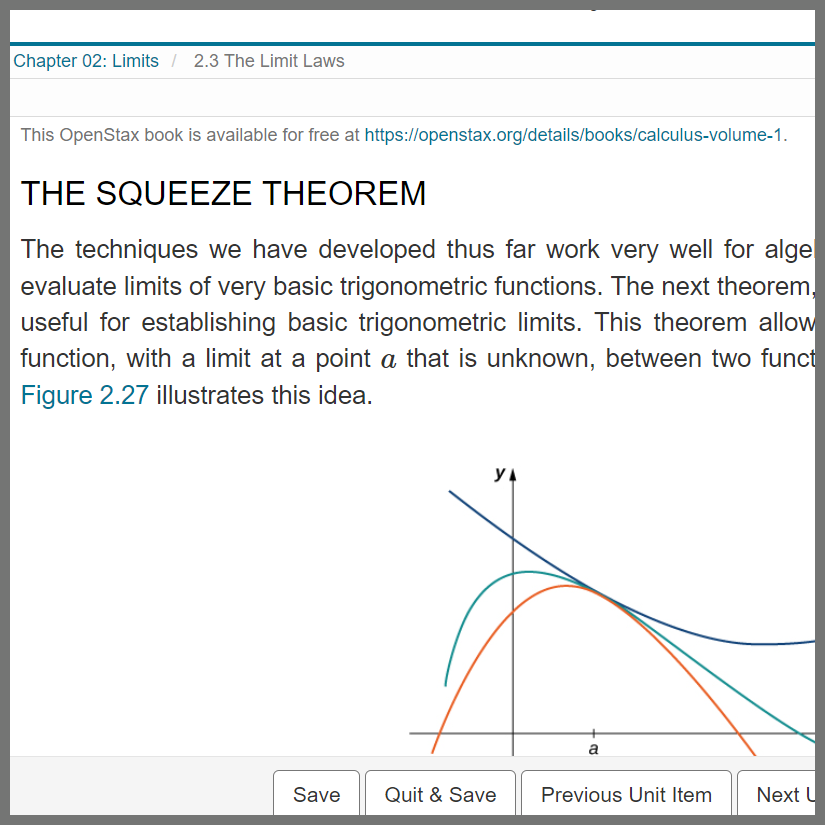
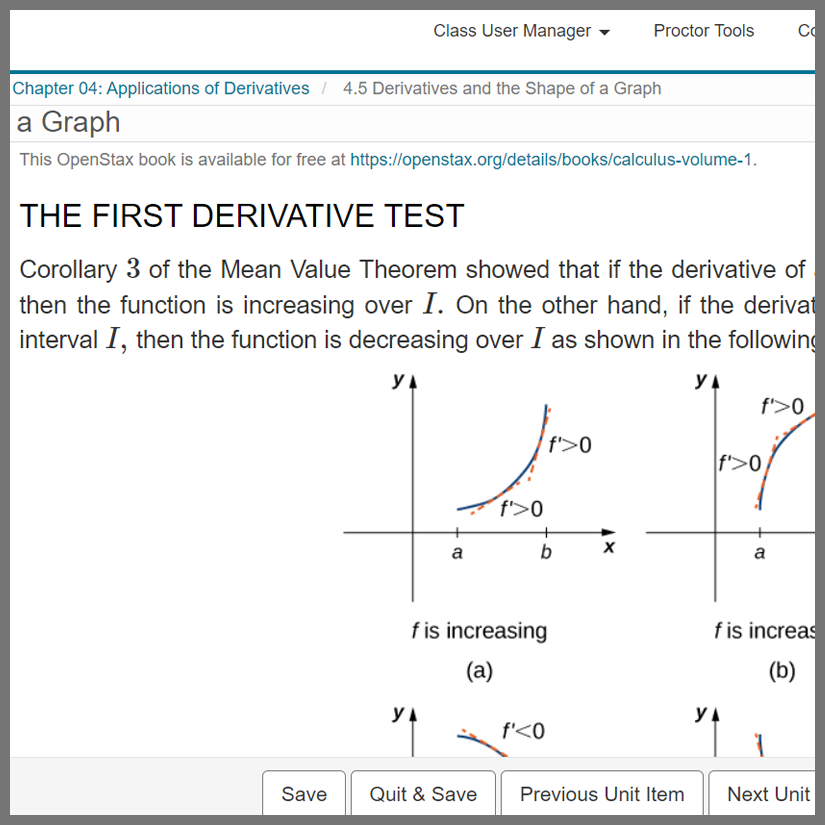
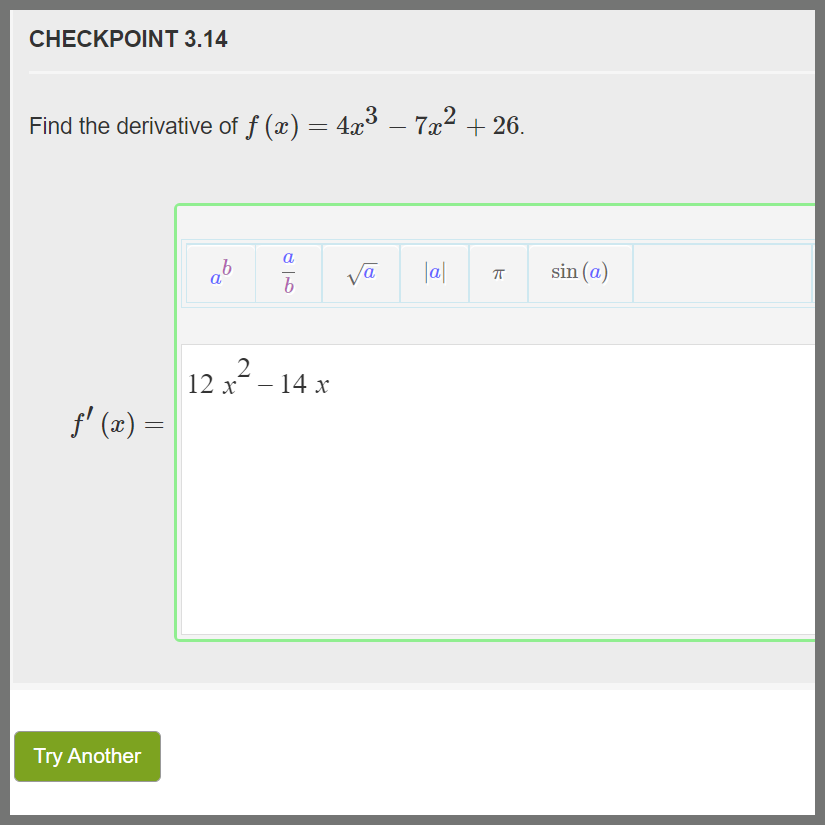
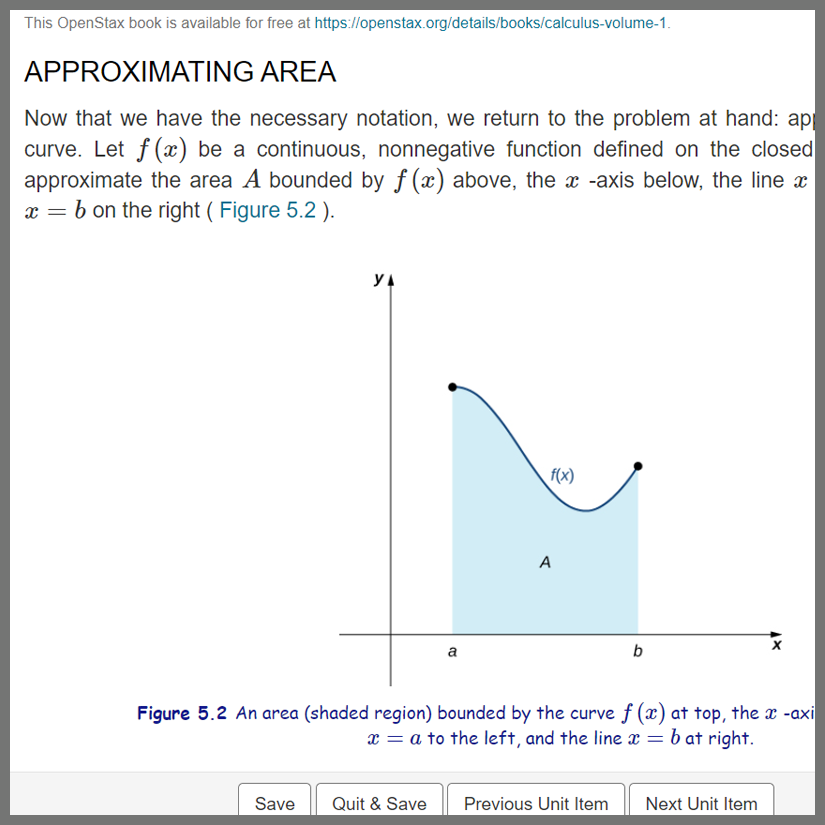
Description

The Calculus Volume 1 Content Pack is one of three OpenStax Calculus offerings that you can use as a customizable starting point to a complete calculus course in Möbius. OpenStax Calculus covers the core concepts of calculus and helps students understand how those concepts apply to their lives and the world around them. Due to the comprehensive nature of the material, OpenStax Calculus with Möbius is offered as a typical two- or three-semester general calculus course, with Volume 1 covering: functions, limits, derivatives, and integration. This customizable resource includes all traditional OpenStax features such as chapter introductions, sections, review material, and practice tests, and has been enhanced with Möbius capabilities including algorithmic questions, in-lesson questions with unlimited practice, helpful hints, and immediate feedback.

How does Möbius take OpenStax to the next level?

Course Structure

  • All content is organized into 8 units for easy navigation
  • Course materials provide a solid foundation for creating your course offering which include 58 lessons with illustrative visualizations, unlimited practice, helpful hints, and immediate feedback to promote Active Learning
  • Create different forms of assessment materials to evaluate student comprehension through a variety of different question types
  • Pull from a vast selection of over 900 questions that you can use to create your own course materials or supplement existing ones
8 units
58 lessons
0 assignments
900+ questions

Introductory Materials

Unit 1: Functions and Graphs

  • 1.1 Review of Functions

  • 1.2 Basic Classes of Functions

  • 1.3 Trigonometric Functions

  • 1.4 Inverse Functions

  • 1.5 Exponential and Logarithmic Functions

Unit 2: Limits

  • 2.1 A Preview of Calculus

  • 2.2 The Limit of a Function

  • 2.3 The Limit Laws

  • 2.4 Continuity

  • 2.5 The Precise Definition of a Limit

Unit 3: Derivatives

  • 3.1 Defining the Derivative

  • 3.2 The Derivative as a Function

  • 3.3 Differentiation Rules

  • 3.4 Derivatives as Rates of Change

  • 3.5 Derivatives of Trigonometric Functions

  • 3.6 The Chain Rule

  • 3.7 Derivatives of Inverse Functions

  • 3.8 Implicit Differentiation

  • 3.9 Derivatives of Exponential and Logarithmic Functions

Unit 4: Applications of Derivatives

  • 4.1 Related Rates

  • 4.2 Linear Approximations and Differentials

  • 4.3 Maxima and Minima

  • 4.4 The Mean Value Theorem

  • 4.5 Derivatives and the Shape of a Graph

  • 4.6 Limits at Infinity and Asymptotes

  • 4.7 Applied Optimization Problems

  • 4.8 L’Hôpital’s Rule

  • 4.9 Newton’s Method

  • 4.10 Antiderivatives

Unit 5: Integration

  • 5.1 Approximating Areas

  • 5.2 The Definite Integral

  • 5.3 The Fundamental Theorem of Calculus

  • 5.4 Integration Formulas and the Net Change Theorem

  • 5.5 Substitution

  • 5.6 Integrals Involving Exponential and Logarithmic Functions

  • 5.7 Integrals Resulting in Inverse Trigonometric Functions

Unit 6: Applications of Integration

  • 6.1 Areas between Curves

  • 6.2 Determining Volumes by Slicing

  • 6.3 Volumes of Revolution: Cylindrical Shells

  • 6.4 Arc Length of a Curve and Surface Area

  • 6.5 Physical Applications

  • 6.6 Moments and Centers of Mass

  • 6.7 Integrals, Exponential Functions, and Logarithms

  • 6.8 Exponential Growth and Decay

  • 6.9 Calculus of the Hyperbolic

Appendices

Back to Menu

Want a closer look at this Content Pack?

Our Möbius experts can show you the capabilities of any of our Content Packs. During this complimentary, customized demonstration, you’ll discover how Möbius can elevate your online course delivery for STEM subjects.

Contact us to Learn More

Content Packs That May Interest You

Precalculus

Calculus Volume 2

Calculus Volume 3

Browse Content Catalogue

Experience Möbius from
your students’ perspective

Try it Now
DigitalEd